拼手气红包的公平性

关于实现一个微信抢红包的思路是如何呢，我们应该从这么几个角度分析

随机性
公平性
期望值（每个人都期望拿到剩余红包的全部）

观察下这个方法能否做到上诉所说的呢

function faultyRedPacket(total, num) {
  const result = [];
  let rest = total;
  
  for (let i = 0; i < num - 1; i++) {
    // 简单随机：0.01 ~ 剩余金额
    const amount = (Math.random() * rest).toFixed(2);
    rest -= amount;
    result.push(amount);
  }
  
  result.push(rest.toFixed(2));
  return result;
}

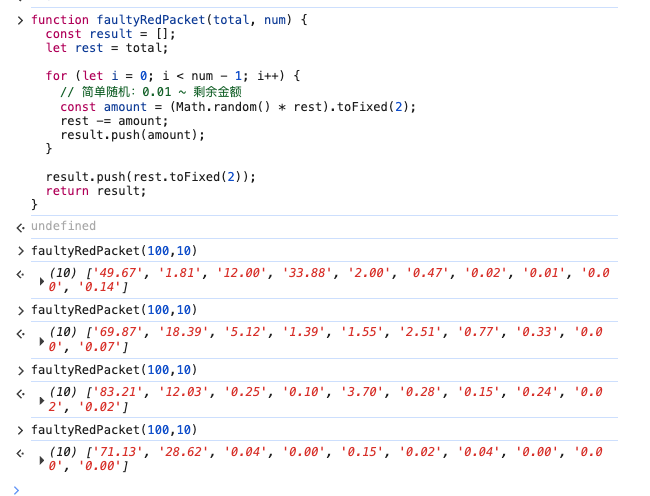
通过测试可以发现，越早抢红包的人金额越大，还会出现有人抢不到的情况，也就违背了公平性原则

二倍均值法

function wechatRedPacket(total, num) {
  // 转换为分处理，避免浮点精度问题
  let rest = Math.round(total * 100);
  const result = [];
  
  for (let i = 0; i < num - 1; i++) {
    // 核心算法：随机范围 = 剩余人均值 * 2
    const max = Math.floor(rest / (num - i) * 2);
    let amount = Math.floor(Math.random() * max) + 1;
    console.log("amount----",amount)
    // 保证剩余金额足够
    amount = Math.min(amount, rest - (num - i - 1));
    
    rest -= amount;
    result.push((amount / 100).toFixed(2));
  }
  
  result.push((rest / 100).toFixed(2));
  return result;
}

可以看到这种模式就比较公平了

核心思想

动态调整上限：
- 每次随机范围 = 剩余金额 / 剩余人数 × 2
- 例如：100元分给10人，第一个红包上限 = (100/10)×2 = 20元
保底机制：
- 确保剩余金额足够剩余人数每人至少0.01元
- amount = Math.min(amount, rest - (num - i - 1))
整数运算：
- 所有计算以"分"为单位，避免浮点数精度问题
- 最终结果再转换为元

为什么这种模式一定就是公平的呢？

设剩余金额为M，剩余人数为N，则：

随机金额范围：[0.01, 2M/N] 期望值 E = (0.01 + 2M/N) / 2 = M/N 所有人抢到金额的期望值严格相等！这就是二倍均值法的精妙之处。

为什么不是完全随机？

完全随机分配可能导致：

有人抢到0.01元，有人抢到99元
最后几个红包可能为负数
整体分布不均匀

微信红包追求的是"相对公平的随机"：

最大值不超过平均值的2倍
最小值不低于0.01元
所有人金额期望值相等

拼手气红包的公平性

二倍均值法 ​

核心思想 ​

二倍均值法

核心思想